Like most first-year teachers, I couldn’t believe some of the gaps in my kids’ knowledge. My geometry students scowled at word problems, mangled the distributive property, and handled fractions with the same fondness you’d show a steaming diaper. Privately, I grumbled. Why didn’t their old teachers cover this stuff properly? Why is it my job to pick up the pieces?
Two years later, I got the chance to teach the same kids trigonometry. I still couldn’t believe some of the holes in their background. What’s their problem with special right triangles? Where’s their intuition about proof? Why didn’t they learn this stuff? As soon as I found myself blaming the last guy, I realized.
The last guy was me.
I’m not sure “blame” has any useful place in a teacher’s philosophy. When a student enters my class, the epic story of her education has been unfolding for years. Her teachers have helped and harmed her in a thousand subtle and inseparable ways. They’ve built or shattered her confidence, kindled or snuffed her love of learning, warped or reinforced her structures of knowledge. How am I to tell the allies from the villains in that complex and shifting tale? My role is not to bring charges against my predecessors. My role is to find what snags and pitfalls are holding our hero back, and to help her along her journey.
I’m not the protagonist in her story. She is.
This year, as a private tutor, I struggle to follow my own advice. “Your teacher’s only given four homework assignments all year?” “You still haven’t gotten back that test from two months ago?” “He’s bothering with those useless product-to-sum trig formulas?” As a tutor, I get to peek into a dozen different classrooms, and I’m often discouraged by what I see. Blame creeps into my thoughts.
Then I remember what it’s like to teach: the long hours, the stacks to grade, the scramble to plan a half-decent lesson and the self-loathing when I know I’ve fallen short. I try to forgive my tutees’ teachers, knowing I’ll be back in their shoes soon enough, just as ripe for blame.
I’m reminded of one of my favorite stories. (It’s probably apocryphal, but so are all the best ones.) Brezhnev takes control in Russia, and the day before he enters office, his predecessor Krushchev (deposed and disgraced) hands him two letters.
“When you run into serious trouble, open the first envelope,” Krushchev says. “And when it happens again, open the second one.”
After a while, trouble comes, and Brezhnev fears he’ll be forced from office. He opens envelope #1, and finds a note that says:
So Brezhnev blames his predecessor, and it works like a charm, everyone letting him off the hook. A few years later, a second crisis arrives, so Brezhnev eagerly opens letter #2, hoping for another solution to bail him out. The note says:
There’s only so long you can blame the last guy. Sooner or later, the last guy is you.
P.S. In dwelling on the gaps in my students’ knowledge, I’ve vastly underrated what bright and witty and wonderful people they are. If you want an honest picture of them, just imagine the kindest, most diligent imps you’ve ever met. They still hate fractions. And I still love ’em.






I’ve also found that it’s easy to forget how much (or how little) students have seen of a particular concept. When we ask ourselves, “why don’t they remember special right triangles?”, it may because the concept was only introduced IN the previous year, for one day out of 365. Even if more emphasis was put on it (thus taking away time to emphasize something else), that’s still MAYBE 1% of the entire year, a year that also involves English and Science and who knows what else taking place outside of school, not to mention all the years before when that concept DIDN’T appear. Memory is a curious thing, and blame really doesn’t get us anywhere.
Interesting story about the letters, by the way, hadn’t heard that. Or if I had, I’ve since forgotten.
Yeah, that’s really true. I have to catch myself saying, “Did your teacher cover this in Algebra 2?!” Because it’s perfectly possible that their teacher did, and that the students did well with it, and that it’s just slipped from their memory in the year since.
Wikipedia’s article on special right triangles says: “A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist.” I submit that no reasonable person is going to memorize exactly which regular features and simple formulas count towards specialness.
Except it’s pretty easy! The only two that really matter are the triangle which is half a square, and the triangle which is half of an equilateral triangle.
By the way, Brezhnev died in office (his last two years were pretty ineffectual due to alcoholism, emphysema, and circulatory problems), but the story’s still a good one!
Ah, thanks! Good to know. I should try to persuade some world leaders to reenact this story, just so we can give it specific, accurate names (instead of couching it as apocrypha.)
I heard that two letters story before, but I didn’t know it was Krushchev. Interesting!
Not that it matters, but I believe “riddance” is spelled with an ‘a’.
Uh-oh. Fixing that spelling mistake in those two drawings will require Photoshopping skills beyond my abilities…
…a little help, anyone?
It’s “riddance”.
I like this post because it reminds me to avoid looking at students from a deficit perspective–what they can’t do, of which there’s plenty–vs what they can do, what they have inside of them, and what they are capable of becoming. Looking forward has always served my students better than looking back.
Well said. I like to think in terms of “next steps”: “You can do X, so let me teach you how to do X + 1.” This approach is sometimes tough to reconcile with rigid curricula or the needs of a particular course… but it’s a helpful framework.
My first reaction to this is a story from the first school where I taught. It was a small 6 – 12 school with separate buildings for middle and high school. The high school was small enough that teachers often popped into each others’ classrooms. I was teaching precalc and calculus and was the only one doing so. When the physics teacher would refer to some trig concept or something to do with distance/velocity/acceleration ideas he would often encounter students who ‘knew’ this stuff from my classroom claiming otherwise. He would ask them if he should fetch me to join the conversation. Most of the time they would sigh and admit that they had some knowledge after all. In reflecting on this situation for years I have come to a couple of conclusions – (1) In a new context, or with time passing, people (not just our students) will have a hard time recalling and reorganizing information effectively (2) When a topic is discussed by a different person with different emphasis on what/how to say things, it is easy to convince yourself that you don’t actually have the knowledge that you need in this new context (3) It’s easier to say you don’t remember something and have it explained all over again than it is to recall and reorganize that information yourself.
Mmm, I think those are all wise lessons to draw.
Another takeaway, for me, is the benefit of having different teachers over the course of your education. There are aspects of math that I downplay or overlook or am just not very good at teaching. Having other teachers addressing related ideas later allows students to make their own connections, and synthesize the best of what different teachers can offer.
It’s also very true that familiar ideas can feel unfamiliar in a slightly different context. I’ve had it happen often that someone begins a story and asks, “Have I told you this already?” I say no, only to recognize the anecdote a moment later.
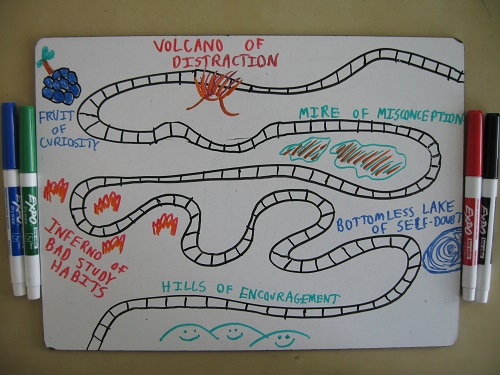
This is very valuable advice to keep in mind, whether we are math teachers, teachers of less cool subjects than math, or parents: “My role is not to bring charges against my predecessors. My role is to find what snags and pitfalls are holding our hero back, and to help her along her journey. I’m not the protagonist in her story. She is.” I especially love the Candyland map of the journey.
Is it possible that “riddence” is the proper spelling of “riddance” uttered in a thick Russian accent? 😉
Yeah, let’s go with that. 😉
As a parent and a former math student I can relate to this.
This story makes me think of all the crazy and frustrating math class stories my daughter brings home from her freshman year in high school. Thank goodness she found a good blameless tutor.
Hope to see a lot more from you in 2014. I’m really enjoying your blog!
Thanks for reading, Juliette! Glad to hear your daughter found a good tutor.
My first year I was like this as the shock of what the students know and did not know amazed me. I love when my trig students show up in calc and they have forgotten all the trig stuff I say, “Man your trig teacher was an incompetent moron, but don’t worry you’re in much better hands now.” I love the evolving emotion on their face as they realize: 1. I said something mean, 2. They figure out who I insulted – their former teacher, and 3. The moment when they realize I was their former teacher…I have found this is a great way to measure how fast kids can think on their feet, but it’s also just silly fun.
Definitely! I’ve used that line, too, in exactly the same context. “C’mon, guys, sine of 3 pi over 4? You can’t do this? You must have had a terrible trig class.”
My wife is a biology teacher, always working and always complaining about her students. There are a few great ones but many have no business being in a high school biology class. Even some of her IB students are in the wrong class.
I think you mentioned that there are so many things to learn and so little time for students to learn them. Everyone’s mind doesn’t instantly absorb a concept and sit ready for the next one to be tossed it’s way. I think for many people it takes repetition and practice in order to grasp a concept, and our schools to not allow for this.
I think we need longer school days and longer school years.
What are your thoughts on the Khan Academy? They propose that students watch the classes on line and then spend class time working on the home work. That way when a student gets stuck the teacher can help. I remember sitting at home doing homework by my self and being stuck. For most students if you’re stuck, you’re stuck. They need a teacher’s help to figure it out and move forward.
Yeah, I’m definitely with you on a longer schoolyear. Longer schoolday I’m less sure about – I can see arguments on both sides.
Khan Academy definitely provides a cool service. There are a lot of teachers (at K-12 and at college level) working to create a “flipped classroom,” as you describe.
I think it has some potential advantages over the conventional classroom. I think it has some potential disadvantages, too, including:
1. In a good conventional classroom, you don’t have long stretches of lecture. You have a lot of back-and-forth and interaction. The flipped classroom inevitably introduces you to material with a long stretch of passive lecture.
2. First exposure to material is, in my experience, super important for avoiding misconceptions and building around deep ideas. It’s harder to make sure this happens if the kids aren’t there in front of me.
I think a “mixed” classroom may be the best solution: both at school and at home, have kids do a mixture of passive and active learning.
You are probably right. It seems like a really cool idea and I see the merits of this approach.
I wish I had something like this when I was in school. When I was sitting at the kitchen table doing my homework, if I got stuck I was stuck. I’ve encouraged my daughter to use Khan, but I’m Dad.
Reblogged this on Oblivion – Resurrected.
Product to sum trigonometric formulas are not useless. This is why radio transmitters and receivers work. Take the carrier wave: sin At. Multiply it by the signal from the content, which breaks down into various sine waves: sin wt. The product is the sum of various sine waves:
sin (A + w)t and sin(A-w)t and cos(A+w)t and cos (A-w)t. A is much larger than w, so tbe broadcast has a small spread of frequencies near A. Your receiver, tuned to A, picks all of them up.
That’s a cool application! Didn’t know about that.
By “useless,” I didn’t necessarily mean “useless in the larger world,” but “a waste of time for 11th graders to memorize.” I ask students to memorize a handful of formulas (cos(a+b) = cos(a)cos(b) – sin(a)sin(b), for example), prove a handful of others (like cos(2a) = cos^2(a) = sin^2(b)), and for the others, just know that they’re out there if you need to look ’em up.
I’ve seen too many cases where teachers do not know how their subjects are used in real life, and where students are convinced that their math courses are just games devoted to deciding who gets to be a pre-med. I remember from my teaching days the dread question “Will this be on the exam, Professor Jablow?” Usually this was when i as trying to get beyond the textbook. For example the week we discussed integrals of the form $\int_-\pi^\pi \cos nx \sin mx\,dx$, I would always relate this to Fourier analysis and Fourier series, and how their music CDs were made. This led always to annoyed students.
I agree that applications are important and valuable, but I think that your implied dichotomy of “knowing how the subject is used in real life” versus “just games devoted to deciding who gets to be a pre-med” is a false one. I come at things more from a pure side, driving hard at proof, argument, deduction, etc. It’s a mathematician’s perspective, rather than a scientist’s. I think it’s important that both the pure and applied side of mathematics come across in K-12 education, so I don’t buy your connection between a lack of applications and the pre-med “will this be on the test?” perspective.