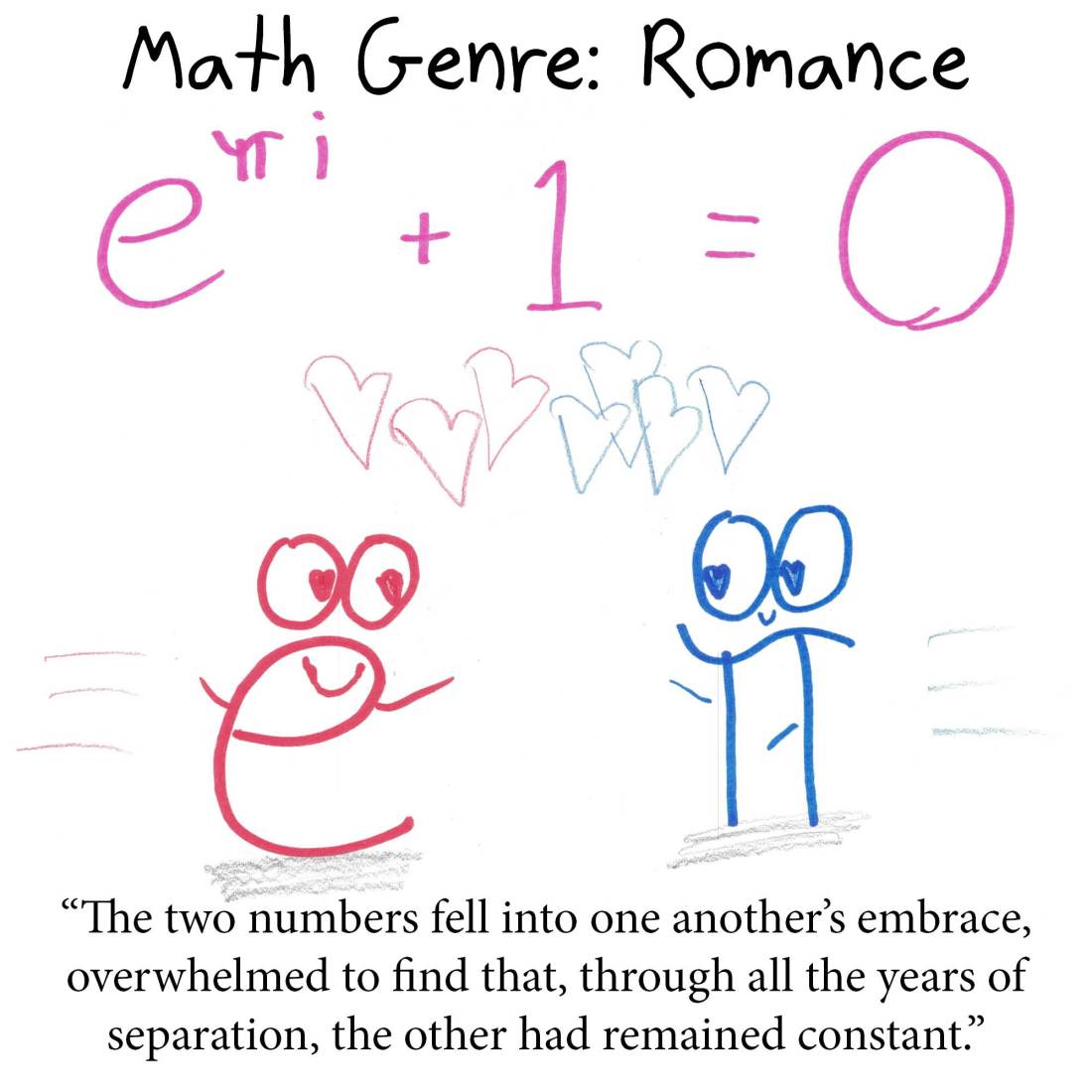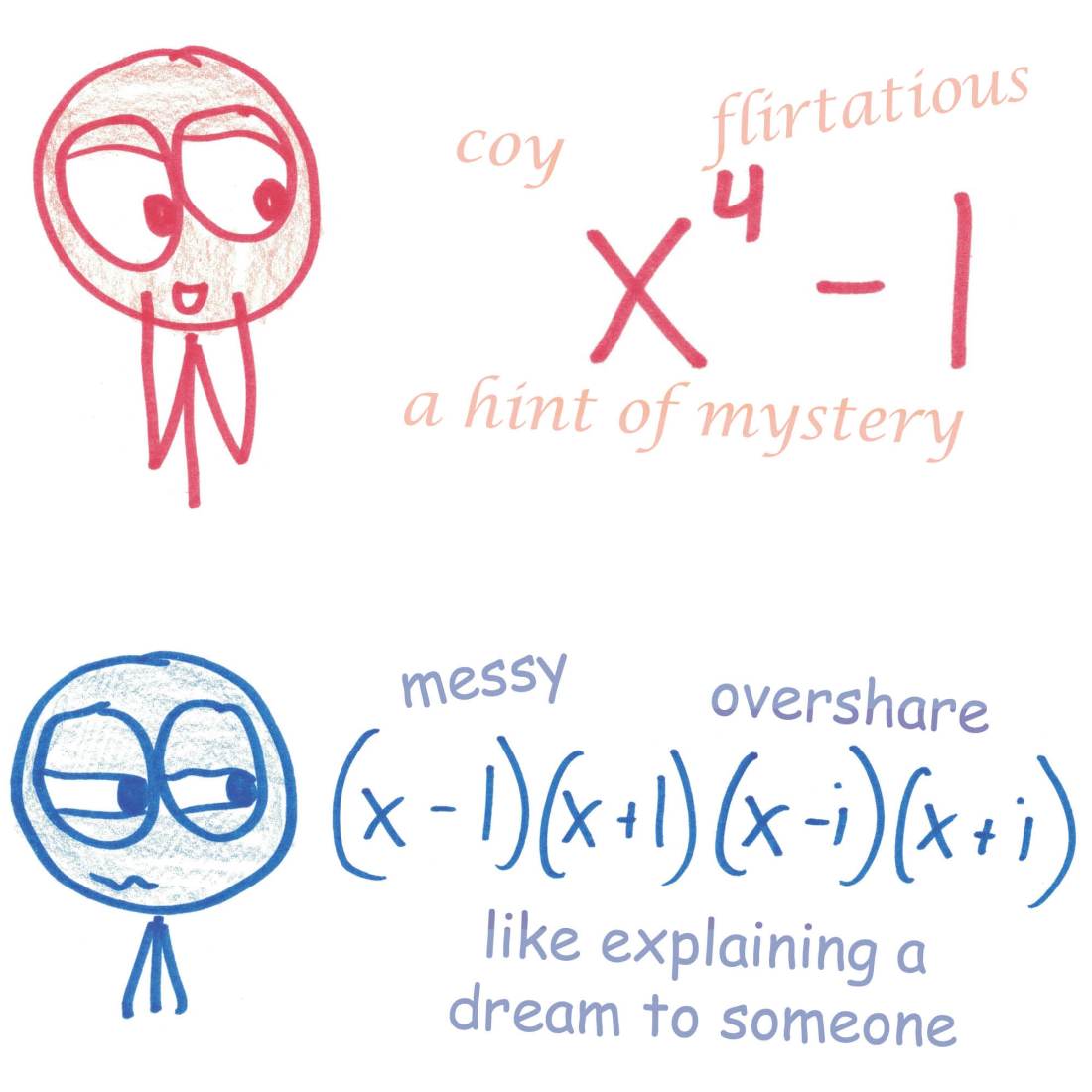A guide for teachers looking to fix up their test scores.
Curves to curve by.
10 best triangles of the 21st century (so far).
The definitive ranking.
Oxbridge of America
A plea, not to end snap judgments, but merely to better calibrate them.
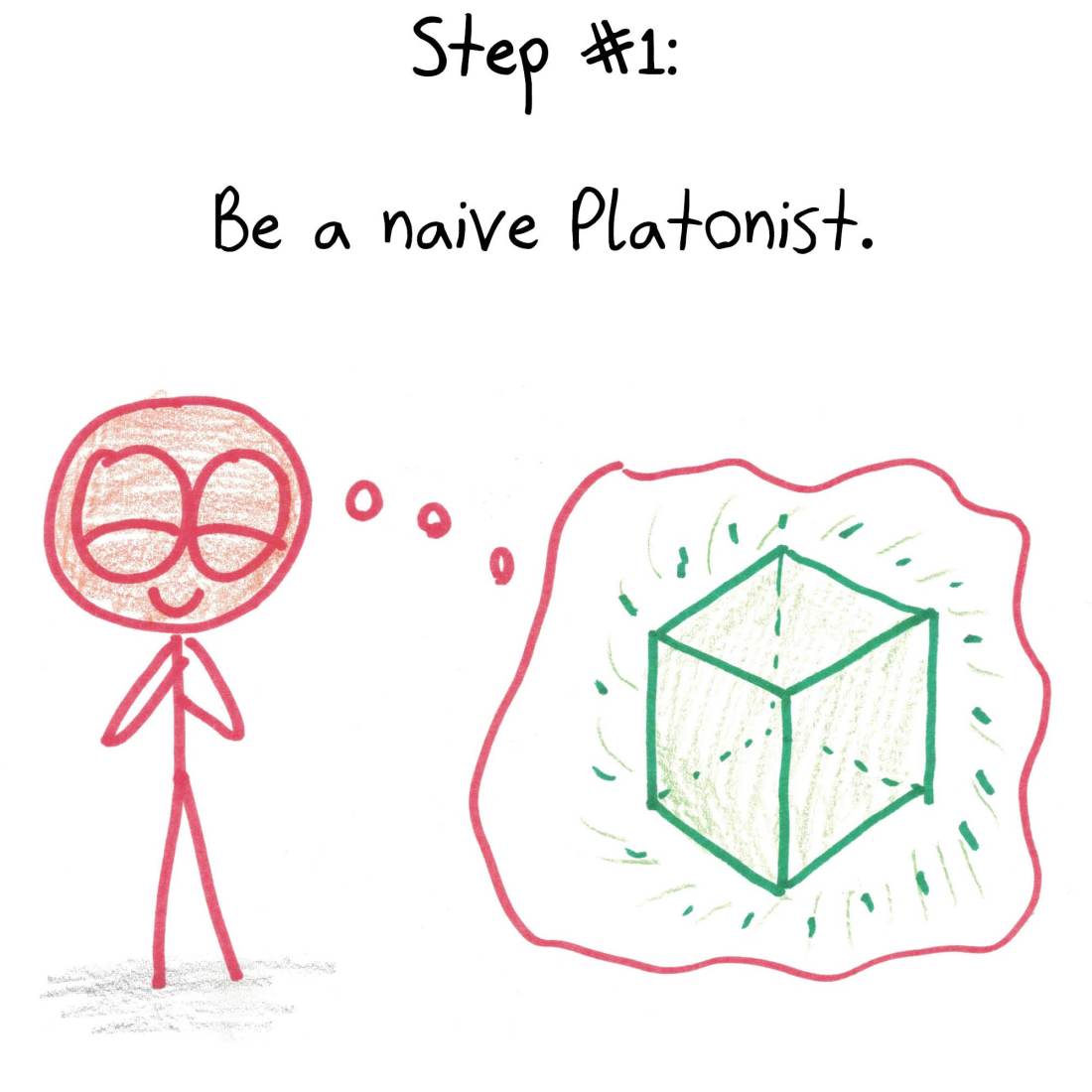
Is math discovered or invented?
Four completely satisfying answers.
The mathematics of “are we there yet?”
Will the Marvel Cinematic Universe outlast human civilization? Unlikely, but not impossible.
Ask the Algorithm
Life advice from the source of all wisdom.
A mathematician’s coming-of-age story.
The six steps to wisdom.
Literary genres as equations.
Come tour the bookstore of equations.
Fashion tips for writing math.
Forget "clear" and "correct" math. Let's learn to write it with panache.
A world without zero. (February 2025 in bad drawings)
The inaugural math puzzle for Science News.