a one-question quiz
I’ll be the first to admit that a single question cannot summarize your entire personality. For that, you’d need three or four questions, minimum. Plus they would need to appear in the pages of Cosmo.
Still, for one question on the internet, I find this one illuminating.
Here’s the idea. I’m going to give you a single lottery ticket. It will pay you a prize of N dollars, with probability 1/N. The twist: you get to pick the value of N.
With no right answers—each ticket, after all, has an expected value of $1—the game functions as a kind of personality test. Do you prefer safety or risk? How risky will you go?
In the past, I’ve collected over 700 answers, which have revealed four basic and extremely scientific personality types:
Rational Killjoys (roughly 1 in 3 people). They pick N = 1, taking a lottery ticket that pays out a guaranteed $1. I can’t tell if these people are smart or boring. Maybe smartness is boring. Still, I admire the logic of Jessamyn Dukes: “Given how delighted I am when I find a dollar in my pocket from past me,” Jessamyn explained, “I pick N = 1. Guaranteed free dollar and tiny serotonin boost? Sold.”
Seekers of Small Adventures (roughly 1 in 4 people). They pick N between 1 and 1000. It’s not quit-your-job money; just enough to make the game fun. “That would be enough to really enjoy winning,” explained Julie Wright, “but the odds of winning are at least a little believable.”
Dreaming Debtors (roughly 1 in 5 people).They pick N between 1000 and 1,000,000, often hoping for a specific and life-changing amount of money. Kevin Weatherwalks, for example, picked N = 60,000, calling it a “freeroll for a chance to cancel my student debt.”
Lovers of Big Numbers (roughly 1 in 5 people). They pick N greater than a million, effectively choosing an ordinary lottery ticket—or, in some cases, an extraordinary lottery ticket, with a payoff 1000 times higher and odds 1000 times longer. “I will play at max levels,” pledged one.
As for me? It depends on my mood. Most of the time I’m a killjoy, but every now and then, I might pick N = 1 trillion, just to hold in my hand the momentary possibility of wealth beyond imagination…
….until, with probability 99.9999999999%, it collapses down to nothingness.
As a “Rational Killjoy”, my arguement for N=1 is the fact that money has diminishing returns. A million dollars is not actually a million times as useful as 1 dollar, because you run out of important things to spend money on. Thus, even though the expected number of dollars from the ticket is the same for all values of N, the expected utility decreases as N increases.
How is it a diminishing return? So are you saying over the course of your lifetime, that, even living frugally, you will not spend $1,000,000? If older and you have 20 years left to live, so $50,000/year probably would cover the, as you say, “important things” (housing, food, medical, …), but certainly would not be much more than a frugal life style. If you are younger, and have more years left, it would not last. You seem to assume you have to spend it all at once, not doing the truly rational thing which would be to invest it for a lifetime (supplemental?) income. If that truly becomes income you do not need or want to spend, there are many philanthropic uses at which you can put the money to use.
“Important things”??? Why would I waste a million dollars on important things, I’d buy fun things.
I feel like I would pick an extremely large value of N. If N = 1 billion and I win, my life will be much more changed than if N = 1 and I get a dollar. In other words, a billion dollars is a much bigger life changer than 1 dollar.
First of all, love the concept and your writing always makes me smile!
Also, I’d probably be a small adventure seeker- anything greater than 1 in 1000 chance seems so unlikely that I wouldn’t even think about winning. Maybe 200 dollars would be a good amount to win without being ludicrous- I could treat myself but it’s not never going to happen.
There are arguments for all options but that’s me I guess.
Imma pick N = 1/2
How would that even pay? You’d get two wins of $0.50 each? I think it’s more likely the lottery company would throw it out.
I tried that as well – but only after trying N=0 😉
Then I thought of a gogoolplex….. And then I settled for some 999,999,999,999 – enough to help with climate, pandemics, world hunger (and a new pc).
2,000,000 Unless it’s life changing, why bother?
I pick $1 because I could see that they all had an expected value of $1 so I might as well get it for sure.
I attempted to fill out the form with 1/2 (“You may choose any value of N that you like”) but the form is all “Please pick a valid number!” I can’t even submit it as 0.5.
(I filled out the form the sensible way, with $1.)
Thinking from a different perspective, what’s the best prize distribution to benefit…. Well to benefit who?
One huge prize. A big prize and some smaller. Lots of little one and all points in between…..
Thinking of the U.K. lottery there is a prize distribution but it’s heavily to one big and loads of little.
What benefits society the most? !!! If one person gets a huge prize most of the money won’t be spent…… overall economic benefit is actually small. Give the same amount to lots of people… they’ll spend lots of it. Bigger economic kick. More people ultimately benefit!?
I’ve not expressed this well but what I’m trying to get at is what prize distribution gives the best societal impact in terms of stimulating the economy…… or are there other considerations????
I’m uncertain and confused. Can others provide insights????
How much does the lottery ticket cost?
I ask because the density is a Harmonic Series and, so, diverges. That means the expectation of the payoff does not exist. Indeed, any General Harmonic Series diverges as well, viz.,
where
is nonzero, and 
is not zero and not a negative integer.
Curiously, the Random Harmonic Series
where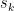
are each i.i.d. random variables on the domain 
weighted each a half does converge.
The convergence of the harmonic series is utterly immaterial. You’re not buying a ticket that pays you a varying amount based on a parameter. You’re buying ONE ticket with ONE payout. There’s no series to be added.
But if “What is the payout of this ticket?” is an ill-defined question, then the problem is nonsensical. Also, if the original seller of the ticket, who is presumably the same entity which makes the payout, has finite resources there has to be an upper bound on n. That’s why I asked what the original ticket cost. And if the original ticket cost an infinite amount to defend against a choice of an arbitrarily large n, I say the question is bupkis.
I think you’re picturing a more complicated question than the one I had in mind!
I’m giving you the ticket for free. You get precisely one ticket.
The ticket is constructed to have an expected value of $1. That is, it pays out $n with probability 1/n. It does this for some specific value of n.
The question is just what value of n you pick!
Hi Ben,
Well, then, my “personality” says if I haven’t constraints on N from the problem, I’m going to pick N using a random device. If N is unbounded that’ll be an interesting, although not impossible charge. But any personal pick is subject to the same constraints.
I don’t buy the idea of going big to win. I don’t do lotteries.
Fair enough – though if you don’t do lotteries, then you can just let N = 1 and take the guaranteed dollar!
For lovers of big numbers, the lack of constraints on N might become relevant (e.g., someone might want N = 10^15, which I’m allowing for this question even though, in the unlikely event of someone winning the prize, no real-world institution could afford to pay it). But for people who prefer small N anyway, the potential unboundedness of N doesn’t really matter.
Anyway, I believe “I will choose N randomly” is a very interesting personality type: people who use mathematized randomness to select which kind of mathematized randomness they would like to experience!
Yeah, it’s called a Dirichlet process.
Sorry. My statement “You’re not buying a ticket that pays you a varying amount based on a parameter” is incorrect. That’s EXACTLY what you’re buying. I apologize.
You are correct that the payer does theoretically need infinite resources to deliver what they are promising, if N is left unlimited. If they don’t have infinite resources, then there is definitely the possibility that they cannot deliver, and that affects the sensibility of the problem.
I agree that pricing this ticket is difficult, but the failure of the harmonic series to answer the question just means that another method of pricing must be chosen.
https://bit.ly/3bEHpW2
I feel something to take into consideration is if you have a big (expensive) dream you want to achieve.
Simple example: I want to go to space. Let’s round it and say that a week in the ISS is about 100 million dollars.
If I pick N = 100 000 000$, i get a 0,000 001 % chance of fullfilling this dream.
If I pick anything lower, the chance drop top zero, even if I win. So N=100 millions for me.
I’m not saying that I couldn’t find useful things to spend $1,000,000 on. I could, and I certainly agree that a million dollars is much more useful than $1. Rather my point is that the value of the millionth dollar is not as much as the value of the first dollar. Going from $0 to $500,000 is going from “starving in the streets” (depending on the quality of wellfare in your country) to “able to live frugally off of interest from investment (depending on the cost of living where you live). Going from $500,000 dollars to $1,000,000 still offers you a big improvement in quality of life, but it’s not as big an improvement as the first half million provides. Therefore, the utility that a million dollars provides, while more than the utility of half a million dollars, is not double the utility of half a million dollars (unless you have some very specific life goal that costs a million dollars, as Axel points out). The difference between $1,000,000 and $1,500,000 is even smaller.
If you’re just investing the money to supplement income you already have, then each additional dollar of investment provides less meaningful change in quality of life than the previous one (although a dollar is such a small amount that even the impact of going from $0 to $1 is not very large).
I chose N = 1.5, because:
– N = 1 is no fun, I like to gamble a little.
– N = 2 is too much gamble. I don’t want to take my chances on a coin flip!