or, The World Through Rectangular Glasses
Now that I’m teaching middle school, I find myself wrestling with the sheer number of area formulas that my students need to know (or at least be passingly familiar with). Rectangles, triangles, parallelograms, trapezia…
The logic is this: A handful of geometric figures keep recurring throughout our world. Once you know how to spot them, they’re everywhere, like the Wilhelm Scream. It’s useful to determine the sizes of these shapes effortlessly, via formulas.
That’s all true, so far as it goes. But reducing geometry to formulas alone can lead to tragic misunderstandings, like when a student asked a friend of mine: “Is there a simple way to remember the difference between volume and surface area?” That’s like asking for a simple way to remember the difference between oceans and deserts: You can only confuse them if you have deep misconceptions about each.
So when I teach these formulas, I try to remind myself of an elegant truth: when it comes to area, everything is rectangles.
And yes, I mean everything.
So let’s begin. With rectangles, finding area is a simple matter of multiplication. In each rectangle, you’ve got a little array of squares:
In this case, we have an array of 5 square centimeters by 3 square centimeters. That’s 15 square centimeters in all. Or, more generally: A = bh.
Now, what about triangles?
Well, just draw them inside rectangles.
Notice that we can divide the rectangle into two sides. The triangle fills half of the left sides, and half of the right. So it must be half of the whole area.
Up next: the parallelogram.
Notice that you can chop off one side of the parallelogram, and move it to the other side, giving you…
…a rectangle! So its area is the same as the rectangle’s.
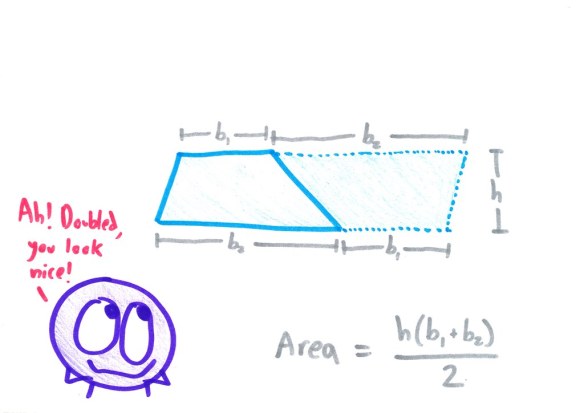
What about the trapezoid (or, as my new British neighbo(u)rs quaintly insist, the trapezium)? This one’s a little trickier.
One method: double the trapezoid, and look at what it makes: a parallelogram!
The area of this whole thing, per our parallelogram formula, is (b1 + b2) x h, but this is two times too big. So we divide by 2 to get our answer.
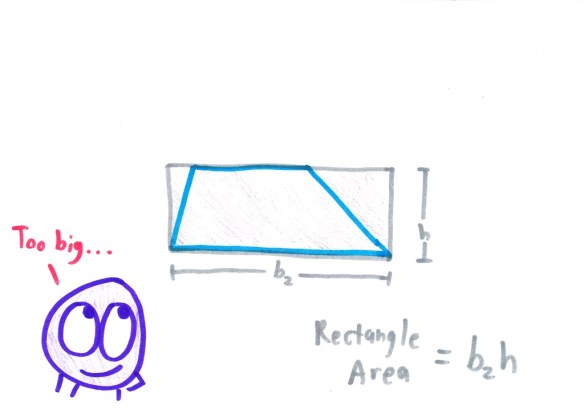
Alternatively, you can notice that the trapezoid has a little rectangle that fits inside…
…and that the trapezoid, in turn, fits inside a bigger rectangle:
The smaller rectangle has area b1h. The larger has area b2h. And the trapezoid is exactly halfway between them. Hence: the same area formula!
Up next: we go fly a kite!
Deploying our by-now-familiar trick, we can fit the kite inside a larger rectangle, and notice that it fills exactly half:
Hence, our formula: the area is d1d2/2.
What about a rhombus? The same trick!
If you recall that a square is both a special rectangle (because its angles are all equal) and a special rhombus (because its sides are equal), you’ll see that we can find its area in two ways:
Combining these two formulas, we even get a cool result:
(And you don’t need to phone Pythagoras for help with the proof.)
So far we’ve limited ourselves to simple shapes with straight sides. It’s perhaps not surprising that their areas can be found by the clever application of rectangles. But what about something more exotic, something less obviously rectangular?
What about, say… the circle?
First, slice your circle up like a pizza. Then, rearrange the slices in an alternating pattern, to get a shape like this:
It looks kind of like a parallelogram, right? It has a “height” of roughly r (the radius of the circle) and a “base” of roughly πr.
(Note: If you recall, a circle has circumference 2πr. Notice that this base is half the circumference. That’s πr.)
Now, slice it up even finer, and repeat the process. What do you notice?

It looks even more like a parallelogram. And in fact, it’s starting to look like a rectangle.
This is where you draw upon your imagination. Picture slicing the circle up into finer and finer pieces, like a single pizza being shared among the population of the entire world. Then slice it up even finer, so that there’s a slice for every mouse and moose and bacterium on earth. Then slice it up even finer than that!
What will we get?
The finer we slice, the closer we have to a rectangle. And if you could imagine cutting it into “infinite” slices—impossible, but bear with me—you’d get a perfect rectangle.
What would its area be? Well, base times height… which is πr times r… which is πr2. Area formula proved! QED! (That’s Latin for “Game, set, match.”)
Okay. So we’ve boiled the following shapes down to rectangles:
But I promised you that everything was rectangles. And we haven’t covered everything. We haven’t, for example, found the areas of shapes like these:
So, what can we do? Well, we can try to estimate the area of such a shape using one rectangle, but we won’t get very close:
The one on top is too small, and the one on the bottom is too big. And we’ve got no idea how MUCH too big – it isn’t an obvious fraction.
So what do you do when a rectangle fails? Add more rectangles!
Better, but still not great. What about 8 rectangles?
That’s looking closer. And it points towards a pattern: the more skinny rectangles we allow ourselves to use, the closer we get to the true area.
Summarize the whole thing with some equations, and you get an object familiar to calculus students: the integral!
That’s right: the integral. We’re talking about math’s all-powerful engine for finding the area of any shape you can poke an equation at. And the whole thing is nothing but weaponized rectangles.
So, trying to find an area? Put on those rectangular glasses.


























Reblogged this on Adventures of a Teacher Nerdfighter and commented:
Such beauty in mathematics… (I know, “nerd alert,” but it IS beautiful!
Reblogged this on So, You Think You Can Teach ESL?.
Reposted on AtRiUM: At Right Angles, Us and Math https://www.facebook.com/groups/829467740417717/952647844766372/?notif_t=group_activity
as my new British neighbo(u)rs quaintly insist, the trapezium
Quaint it may be, but frankly it makes more sense. The shape with two sides parallel is called a trapezium because it looks like a trapeze, the kind you swing from. The shape with no sides parallel is called a trapezoid because its shape is analogous to, but not the same as, a trapeze (as with humanoid, planetoid, factoid). The U.S. definitions are the result of a mistake in Hutton’s Mathematical Dictionary (1795) which somehow caught on, despite the unanimous testimony of Euclid and everyone following him.
Ah, that’s such better nomenclature! I like the -oid suffix being used that way. This seems to be a case where the British win the point. I may make the switch. (I’m also developing a perverse preference for “zed” over “zee.”)
Your etymology needs a little work.
http://www.etymonline.com/index.php?term=trapezium&allowed_in_frame=0
http://www.etymonline.com/index.php?term=trapezium&allowed_in_frame=0
In short, it has nothing to do with a trapeze, like you swing from.
Nice information
Having always had a rotten memory for “facts”, once I realised that mathematics could be reconstructed at will from a very small number of fairly obvious facts there was no other choice for the future. Sin(A +B) = sin(A)cos(B) + cos(A)sin(B) may have been the least obvious, but it does have a nice symmetry about it !
Agreed! That formula plus even/odd identities and pi/2 – theta identities pretty much cover it.
Great post! There are places, though, where I want to slow down and examine things in more detail (seeing the trajectory of the whole post, I realize you may not have wanted to do that). For instance: does your triangle argument work in all cases? For instance, if we tilt the triangle to an extreme position so that its altitude lies *outside* the triangle — what now? And for the “cut off a triangle” argument re: parallelograms — what if the bases were really far apart? Does the argument still work? (picture (0,0), (5,0), (15,3), (10,3), for example)
In case anyone is interested, here are some Vine posts I made to address these very questions!
https://vine.co/v/OUnn37Yh20A
https://vine.co/v/OxJVj2uQVIF
Nice! I particularly like the parallelogram one. Can you explain what’s happening the triangle one? Not sure I follow the logic.
1. Take an index card and decompose into rectangles R1 and R2 (left to right).
2. Take an (identical) index card and decompose into triangles T1, T2, and T3 (left to right in the video).
Goal: describe the area of T2 (i.e. the non-obvious area) in terms of the other shapes. [We secretly believe that it is half as large as the rectangle that shares the same base and height, i.e. half of R2 — but why?]
3. T1+T2 = T3
4. T3 = half of (R1+R2)
4. T1= half of R1
5. Therefore, the area of T2 must be equal to half of R2!!!
This comes across more clearly with visuals, so I may follow up with an email.
Thanks!
This one was really, really good. It’s just the best blog I’ve seen for quite a long time!
Very good. I liked the use of “weaponised”.
Awesome! 😀
Oh, I don’t think I’ve seen a shape like that before! (referencing the shape drawn under the ellipse in the first picture) What is it?
It’s a segment of a parabola! Archimedes had a good notion of how to find their areas. (He was basically doing integral calculus 1800 years before it was a thing.)
The area of the ellipse looks a bit too big to be right (more than three rectangles, each larger than the ellipse). Did you mean to divide by four?
I will bet that he meant to have the a1 and a2 be like radii, going from center to edge.
Love this post, love your drawings, love your writing!
This will be very helpful, thank you
After you have triangles, the polygons are more easily understood via triangles. Consider the trapezoid or James Key’s extremely sheared parallelogram picture. Just use a diagonal to divide the polygon into two triangles.
I prefer to first discuss squares (look at the units, man: square feet, square meters, etc). Then generalize to rectangles. Then right triangles, and then arbitrary triangles. Now from rectangles and triangles you can conquer the world.
Yeah. Certainly when it comes to proving other properties of polygons (sums of angles, facts about diagonals, etc.) you want to work from triangles. And it would be equally reasonable to start from the square, it being the basic unit of area. I chose rectangles perhaps merely because they make the coolest shape for glasses.
Ingresando comentario
Awesome post as always. I loved the sneaky transition into Calculus! I do the same sort of progression of conceptual area derivations but I use interactive Geogebra files. I find that students remember better when they do the flipping and cutting themselves.
Thank you for the great ideas. I feel inspired to add a little area rant into the beginning of my Calculus unit.
Reblogged this on Miss Burghall's Class and commented:
This ties into and builds upon what we learned in our last unit on measurement.
Thank you Ms. Griffiths for passing this along!
THANKS FOR SUCH OUTSTANDING HELP. MORE GREASE TO YOUR ELBOW. #FREEDOM .E.
Great intuitive explanations. Query though: In the illustration of circle with pizza slices, why is the length of that parallelogram/rectangle equal to Pi * r , and not 2 * Pi * r . Although the formula for area of circle works out fine with Pi * r , but I the length of that parallelogram is the circumference , isn’t it.
Apologies- I got it. When I looked at the drawings, it “occured” to me. although the all slices are of length total circumference is 2 * pi * r, but the length of this parallelogram is made by half the number of pieces 1,3,5,7,11,13. So it is rightly so – Pi * r. math with Not so bad drawing at all! many thanks.
In the first drawing, the formula written inside the ellipse isn’t right. Just nitpicking. Otherwise, great post!